EL PERFIL VELOCIDADES

Señores Académicos, illustres confréres: “hace mucho tiempo, la curiosidad por saber si la visión era más o menos fuerte en el sitio del nervio óptico me llevó a hacer una observación curiosa e inesperada... Pegué sobre un fondo obscuro, poco más o menos a nivel de mis ojos, un círculo de papel blanco, que me serviría como punto de mira fijo, y al mismo tiempo fijé otro a mi lado, hacia mi derecha, a dos pies de distancia del primero, pero algo más abajo… Manteniendo cerrado el ojo izquierdo, me coloqué frente al primer papel y, manteniendo siempre el derecho clavado en él, me fi alejando poco a poco; cuando estuve a nueve pies de distancia aproximadamente, el segundo papel, que tenía como cuatro pulgadas de tamaño, desapareció completamente”⁶¹. Quien así se expresaba en una de las primeras reuniones de la Académie des Sciences era el flamante académico Edme Mariotte, de 46 años, que explicaba a los colegas cómo había logrado descubrir  la presencia de la mancha ciega en la retina. Un experimento tan elemental que cualquiera hubiera podido realizar; pero ¿a quién se le habría ocurrido sino a él, el modesto pero sagaz prior de Saint-Martin–sous-Beaune? Hombre tranquilo, metódico y minucioso, curioso como ningún otro de los secretos de la naturaleza, ese incansable genio de la experimentación empieza a investigar en el laboratorio de la Academia, con igual perspicacia, los fenómenos que más interesan en su época, y a publicar trabajos y más trabajos. Luego de un tratado sobre nivelación, de 1672, produce en 1676 nada menos que cuatro escritos fundamentales: el tratado sobre choque de los cuerpos, donde desarrolla y completa con pruebas experimentales la investigación de Galileo al respecto y presenta un aparato de percusión con bolas de marfil colgantes: el discurso sobre la naturaleza del aire, donde establece la ley fundamental que afirma que la condensación del aire se produce en proporción de los pesos que lo cargan; la memoria sobre la vegetación de las plantas, en la cual, combatiendo las entelequias  y las “causas finales” de los aristotélicos, así como la creencia, común en su tiempo, de que existe un “alma vegetativa” en las plantas (concepto con el que –decía él- los filósofos “no nos vuelven más doctos, porque no nos explican qué es esta alma ni de donde viene”⁶²) investiga los procesos asociados con su alimentación, crecimiento y reproducción; finalmente, el discurso sobre el calor y el frío, donde intenta comprobar que el frío no es, como se pensaba entonces, una substancia o calidad independiente, sino simplemente una privación o disminución del calor. En 1681 aparece el tratado sobre la naturaleza de los colores, en el que Mariotte estudia fenómenos relativos a los rayos solares; allí, entre otras, hallamos la interesante observación de que una lámina de vidrio, mientras se deja atravesar por el calor del sol sin atenuarlo, intercepta casi totalmente el del fuego.

Una de las investigaciones más consistentes y sistemáticas fue la que Mariotte realizó en el campo de la mecánica de los fluidos, investigación cuyos detalles y resultados se publicaron solo en 1686, dos años después de su muerte, en el Traité du mouvement des eaux et des autres corps fluides (Tratado del movimiento de las aguas y de los demás cuerpos fluidos). Los primeros pasos de Mariotte se habían dedicado a repetir los experimentos descritos por Pascal en su Traité de l’équlibre des liqueurs, con el propósito de ver si no se hubiera descuidado algún detalle que valiera la pena volver a examinar: empresa muy propia de esa meticulosidad que lo distinguía. Los ensayos de Pascal eran todos de hidrostática: la “máquina para multiplicar fuerzas”, la presión sobre el fondo de vasos de diferentes formas, el equilibrio de una columna de mercurio con un extremo libre y el otro sumido bajo el agua, el empuje que recibe un disco de cuero en contacto con la extremidad sumergida de un tubo, y el principio de Arquímedes; sin contar otros experimentos con el aire, para estudiar efectos de la presión atmosférica. Una vez repetidos estos experimentos  obtenidos algunos resultados nuevos, Mariotte empezó a estudiar el agua corriente.

Llegó a plantearse el problema que Castelli no había podido resolver; cómo medir velocidades en el seno de un río. “Hay que considerar –escribía- que el agua de un río no avanza con igual velocidad en su superficie y en otras partes, porque cerca del fondo se atrasa mucho al encontrarse con piedras, maleza y otras irregularidades. Esta diferencia de velocidades la comprobé como sigue. Coloqué dos bolsas de cera, atadas a un cordel de un pie de largo, en un riachuelo de flujo uniforme. Una de ellas estaba lastrada en su interior con piedrecitas, para que su peso específico resultara algo mayor que el del agua, la más pesada estiraba el cordel, y hacía que la más liviana se hundiese más bajo de lo que se habría hundido estando sola. De tal suerte, su parte superior quedaba casi a nivel con la superficie libre del agua, así que el viento no podía afectarla. Siempre he notado que la bola inferior queda atrás, especialmente allá donde el fondo del agua había alguna maleza, cerca de la cual pasaba dicha bola; porque ese riachuelo tenía aproximadamente tres pies de profundidad. Pero, si las mismas bolas se colocaban en un sitio donde el agua, encontrándose con algún obstáculo, subía un poco y luego aceleraba su curso, como vemos acontecer bajo los puentes, la bola inferior se adelantaba a la superior; lo que comprobaba que entonces el agua corría más rápido en el centro que en la superficie, Causa de eso es que el agua, al subir un tanto por razón del obstáculo y luego bajar por un declive más inclinado, adquiere más velocidad; el cual movimiento la obliga a sumergirse, hundiéndose más que el declive de la superficie… Por tanto, resulta que en ríos regulares hay siempre grandes cavidades algo bajo de los puentes, … porque el agua que se eleva, al encontrar las pilas del puente se acelera, y pasa violentamente por debajo de la que tiene encima, [dirigiéndose] hacia el fondo de dónde saca arena, la arrastra a un lugar algo más abajo del puente, y allí la amontona…”⁶³

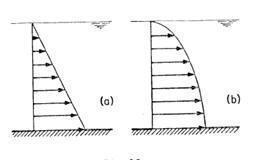
“Además he observado a menudo malezas arrastradas por el agua; y vi claramente que las que estaban dentro del agua, más cerca del fondo, y que habían avanzado más que las [que están] cerca de la superficie, las superiores las sobrepasaban pronto y las dejaban atrás; y si se echaba al mismo río un puñado de recortes de madera pesada, que llegaban al fondo unos antes que otros, siempre he hallado que los más próximos a la superficie se adelantaban a los demás en un orden proporcional, según estaban más o menos lejos del fondo. De los cuales experimentos aparece que, en ríos que escurren libremente, la parte superior del agua corre más rápido que la que está en el centro, y esta más que la que la próxima al fondo; pero que en los ríos forzados a encauzarse en un canal angosto, confinado por ambos lados, en que no haya más que dos o tres pies de agua, el centro avanza más rápido que la superficie.”⁶⁴ Estas aserciones pueden interpretarse en el sentido de que, si indicamos con flechas las velocidades correspondientes a varios puntos de una sección vertical AB de un río y trazamos por sus extremos la curva CD, que es lo      que suele llamar el “perfil de velocidades” vertical, dicho perfil tendría el aspecto que muestra la figura 59a; mientras que en la sección del canal angosto, se parecería al que se ve en la figura 59b.

Cuatro años después del tratado de Mariotte, vio la luz en Italia un nuevo libro dedicado a la medición de las corrientes; estaba escrito en latín y se titulaba Aquarum fluentium mensura nova methodo inquisita (Medición de las aguas corrientes investigada por un método nuevo). Su autor es un médico de 35 años que había sido alumno de Montanari en Bolonia, ciudad de la cual era originario y en cuyo arquigimnasio enseñaban matemáticas: Doménico Guglielmini. ¿Cuáles eran las novedades que ofrecía esta obra con respecto a la de Castelli, ya vieja de 62 años? “Dos dudas se me presentaron en su tratado –escribía Guglielmini-: una fue que, siendo notorio que la velocidad no es la misma ni semejante a sí misma en todas las partes de la corriente, yo no sabía a cuál entre todas tenía que aplicar las demostraciones que él proponía; y aunque fuese fácil darse cuenta de que … se podía sacar un promedio de todas las velocidades, sin embargo quedaba siempre la dificultad mayor, a saber, la de determinar justamente cuál era la velocidad media, lo que me parecía imposible poder deducir de las demostraciones de Castelli. Agregábase, además, la errónea atribución de la velocidad superficial también a las partículas [que estaban] entre el fondo y la superficie, así como la manera dudosa de determinarla; por lo que me parecía que eso no se pudiera sacar nada verdadero ni seguro”, Y luego de haber mencionado que su segunda duda se refería a la famosa proposición de la velocidad doble con tirante doble, anotaba: “Es por eso que empecé realizando experiencias en depósitos, conductos, canales, etc., para averiguar si las velocidades crecen en razón de las alturas, o bien de las raíces de estas. En los tanques, por cierto, halle que se realiza esta última proporción, pero la razón de las velocidades en las secciones de los canales la encontré muy distinta de las dos mencionadas. Esto me llevó a creer que sin duda la velocidad depende muchísimas veces de toda otra causa que no sea la altura del agua en las secciones.”⁶⁵

Si las velocidades fueran creciendo en razón de las  alturas (o sea, de las profundidades por debajo de la superficie), el perfil sería rectilíneo, del tipo de la fig. 60a; si en razón de sus raíces, el perfil sería parabólico, como el de la fig. 60b; Guglielmini había pues llegado a convencerse de que la distribución de velocidades real no se parecía a ninguna de estas dos. Por tanto, se proponía determinar teóricamente el perfil “verdadero”.

El tratado se divide en cinco libros: el primero presenta la “doctrina general” de las velocidades, el segundo considera la medición del agua corriente en canales inclinados aislados, el tercero se refiere a canales horizontales aislados o bien juntos con otros, el cuarto corresponde a canales inclinados simples o múltiples, y el quinto examina modificaciones de los sistemas antes  mencionados. El primer libro es más elemental y detallado que los demás; lo cual se hizo, según dice el autor, “para mayor facilidad, y para adaptarme a la capacidad de los “hidrómetros vulgares”, quienes a lo sumo no conocen de geometría sino los Elementos de Euclides; para que ellos, si no entienden los últimos libros, puedan por lo menos servirse útilmente de este primero. En los siguientes, sabiendo que la materia está por encima de sus conocimientos, he querido ser más sucinto y preciso, en cuanto consideraba dirigirme a los matemáticos más eruditos”.⁶⁶

Luego de haber definido la “velocidad media” en una sección como aquella tal que, si todas las partículas en la sección misma escurriesen con esa velocidad, el gasto no variaría, Guglielmini afirma que el agua que pasa por una sección de un canal inclinado escurre con  la misma velocidad que tendría saliendo de un vaso por un orificio igual a la sección trazada por el principio del canal.⁶⁷ O sea, si AB representa el canal (fig. 61) y AC la horizontal por su principio A, la velocidad media V₁ en la sección B (que se imagina concentrada en un punto) sería aquella con la que saldría el agua por el orificio B abierto en el depósito ADBC, lleno hasta AC. Igual cosa se diría para la velocidad V2 en F, considerando el depósito AEFG, perforado en F. Esta conclusión procede obviamente de considerar al agua como cuerpo grave, que –en ausencia de resistencia- avanza por el canal con movimiento naturalmente acelerado. El cálculo de las velocidades se realizaría simplemente aplicando el teorema de Torricelli.

Hasta aquí, todo bien; pero si el canal fuese horizontal, ¿de dónde saldría la velocidad? En este caso, Guglielmini se ve forzado a tomar en cuenta el tirante de agua, que antes había despreciado. Sean (fig. 62) AB el canal, CE la superficie libre. Coloquemos en D la pantalla DE que detenga el agua, y luego perforémosla, haciendo a un mismo tiempo que por AC siga entrando un gasto igual al que sale. Si las perforaciones son tantas que la pantalla DE se hace toda un agujero, la velocidad con que saldría el agua por DE sería la velocidad media con que el agua abandonaría el vaso CADE a través de dicho orificio. De donde se concluye que la velocidad con la cual el agua escurre por un canal horizontal es igual a aquella con la que saldría de un vaso que esté lleno hasta una altura igual al tirante en el canal.⁶⁸

Finalmente, para determinar perfiles de velocidades en diferentes secciones, Guglielmini traza la parábola de Torricelli, BQ, en la sección inicial AB del canal AE y de ella obtiene las velocidades en las secciones sucesivas CD, EF, etc., tomándolas como iguales a las velocidades de caída en los tramos MN, OP, etc., correspondientes a puntos del mismo nivel en la normal al piso del canal, BP (fig. 63). De aquí infiere que, si se desprecia la resistencia del fondo, la velocidad debe de ser mayor en el fondo que en la superficie, con una razón entre ambas tanto mayor cuanto más cerca del comienzo del canal esté la sección. Como en secciones muy alejadas de este las velocidades se superficie y de fondo se irán aproximando mucho la una a la otra, el autor concluye que prácticamente se podrá suponerlas iguales entre sí.⁶⁹

Imágen obtenida de: http://www.nndb.com/people/112/000095824/

    http://es.wikipedia.org/wiki/Edme_Mariotte

 http://bs-d.unife.it/museologia/matematica/filemat/jpgidr/opidrF14.jpg

 y http://bs-d.unife.it/museologia/matematica/filemat/imgidr/opidrF28.jpg

 y de http://it.wikipedia.org/wiki/File:Domenico_Guglielmini.jpg